Tyler Acorn

Tyler Acorn

Spatial analyst and data scientist with an interest in programming

Speeding up your loops with HashTables/Dict

5 minute read

Today I want to show you a way to speed up your code. If you are like me and are a self taught programmer/coder/data scientist… you are probably pretty comfortable with loops. We all know that loops are “horribly slow” and that you “should never use” them… blah blah blah…. However, for many of us, they are our default approach for a quick and dirt “first draft.” What I want to talk about in this post are hashtables.

Hash tables

So what are hash tables? They are an unorderd collection of key-value pairs. Each key is unique. In python, think of a dictionary, or you could think of a one-dimensional array where your key is the index, but you are not constrained to an integer based index.

If have done any programming in python, you probably know about the dictionary. But have you considered using it like an array? Lets look at an example. I’ll code it up the “quick and dirty loop-de-loop” way and then compare it to using a hash table.

Example

Here’s the example. Write up a function that takes as input two arguments. Arg1 is a list (or 1D array) of integers. Arg2 is a single integer. If any two separate values in your list add up to equal the Arg2 integer, return True. Otherwise return False.

first we’ll look at the quick and dirty approach.

def compare_int_long(intList, testInt):
    """
    compare a list of integers to a single integer.

    return true if any 2 integers (i1 + i2) == testInt
    false otherwise
    """
    for idx1 in range(len(intList)):        # loop through the list
        int1 = intList[idx1]                # grab current integer
        for idx2 in range(len(intList)):    # loop through the list again
            if idx2 != idx1:
                int2 = intList[idx2]        # compare to every other integer
                if int1 + int2 == testInt:
                    return True             # passed test, so return true
    return False                            # failed so return false

This approach works, but is very brute force. For every element in your list, you compare it to every other element in your list to see if it passes the test. The problem with this approach? It scales pretty bad. This, I believe, is an O(N2) complex code. This means the performance of this function increases proportionally to the square of the size of the input list.

Now lets look at an example where we use the hash table (or a dictionary in python). first off though, there are a few things to note. If you create a standard dictionary in python and you call it with an undefined key… you’ll raise an error. For example

temp_dict = {'a': 1, 'b':2}
temp_dict['c']  # raises an error

Defaultdict, however has an interesting property. If you pass it a key with no value, it will assign a default value to that key. So with the above example we can modify it:

temp_dict = defaultdict({'a': 1, 'b':2}, bool)
temp_dict['c']  # returns False

defaultdict makes the above problem much easier to tackle. You could set up a try block to catch any raised errors… or use default dict as shown here.

The other thing to note, is that we need to rethink how we structure the problem. Instead of comparing each integer to every other integer (which is an O(N2) performance problem), we consider a different approach. Our first test was int1 + int2 == testInt. However, we can rearrange the problem to int2 == testInt - int1. This is important because this allows us to do two separate loops through the list instead of a nested loop. Let’s look at the example.

def compare_int_hash(intList, testInt):
    """
    compare a list of integers to a single integer.

    return true if any 2 integers (i1 + i2) == testInt
    false otherwise
    """
    intHash = defaultdict(bool)             # default value will be False
    intCount = defaultdict(int)             # default value will be 0 which is usefull for counting
    listLength = len(intList)

    for idx in range(listLength):           # 1st loop creating a hash table with the key being testInt - int1 and the value being True
        val = testInt - intList[idx]
        intHash[val] = True
        intCount[val] += 1                  # count how many times
    for idx in range(listLength):           # 2nd loop seeing if int2 is found in the hashtable
        if intHash[intList[idx]]:
            if intCount[intList[idx]] > 1:  # do a quick check against the count so we know if we there are 2 values or if we just happen to have a single value that's half the testInt
                return True
    return False

Performance Comparison

The above example is probably more like a O(2N) scale problem. So, now lets take a quick look at the performance of these two functions.

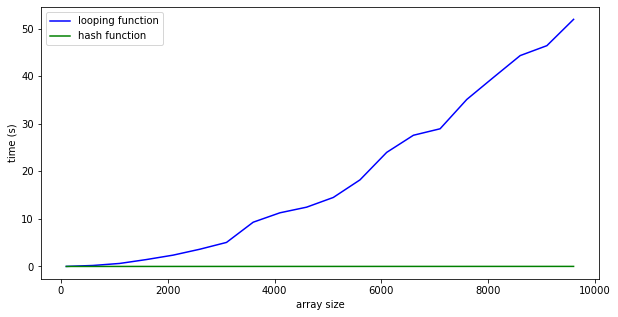
Loopy-De-Loop vs Hashing

As you can see, the loopy-de-loop version very very quickly scales out of control. With just a list of 10,000 elements, worst case scenario, it’ll take you roughly 53 seconds to test. However by using the hash table with the value you are wanting as the index key, you can test that same 10,000 element list in under a second (~0.01 s). Now just because it’s dramatically different doesn’t mean it’s not scaling. There is an issue of scale here.

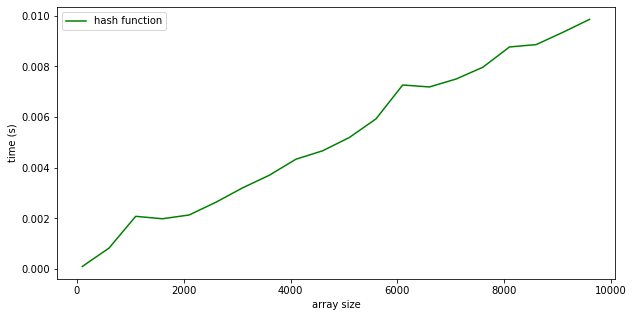
Hash scale

You can see that the hash table approach is still scaling. It’s just more more of a linear increase instead of the exponential scaling of the nested loop.

If you want to play around with the above code, you can check out an example notebook here: Ex_hashtables.ipynb

Or, open up my lessons repo on my binder and navigate to the Ex_hashtables.ipynb file in myBinder’s interactive environment Binder

Hope you enjoyed this quick example!

Further Resources

If you want some further resources or even just have things explained another way, here are a few resources I found useful.

You May Also Enjoy

Setting up jekyll for github pages

1 minute read

The main point of this post is to record some of the settings and theme settings I’ve used for setting up my github.io page. include some of the develop...